Sep 24, 2018
Written by:
Al Hill
Compound returns is one of the most powerful concepts in the world of investing.
Albert Einstein states “Compound interest is the greatest wonder in the world. He who understands it earns it…he who doesn’t pays it.”
Albert Einstein states “Compound interest is the greatest wonder in the world. He who understands it earns it…he who doesn’t pays it.”
I was first introduced to compound returns at church. Before you start bashing my home church, it was not about charging people interest, but the power of compounding returns when investing.
I was about 15 or 16 years old and I had just finished Saturday school. I shamelessly attended a few months in hopes of meeting a cute girl. Look I wasn’t as evolved as I am today.
At any rate, while I was busy learning God’s word, my Dad was in a breakout group with adults learning about the power of compound returns.
He showed me this pamphlet that illustrated the power of compound returns over 20 and 30 years and from that point on I have been hooked on the markets.
I just couldn’t wrap my mind around the fact money could grow to such large sums while I did absolutely nothing in terms of labor.
There are basically three variables or inputs to calculate compound interest: (1) starting principal, (2) expected rate of return and (3) length or period.
Despite being praised by mathematicians and the financial community at large, interest on loans was largely shunned by many of the world’s cultures and religions. Referred to as usury, which is the act of lending at interest or excessive interest was frowned upon and considered an act of enslaving one’s brethren.
Compound interest was able to push through the historical negative connotation and today is a large part of our financial institutions from banking to investing.
When talking about compound interest, it is always best to understand simple interest in order to truly realize its power.
So what is simple interest?
Simple interest is a percentage on your investment paid to you after a fixed period of time – usually one year.
Compound interest, on the other hand, reinvests the interest received at the end of every year or a certain period and thus increasing your capital over time.
For example, if you invested $1,000 in a one year fixed deposit with an annual interest rate of 5%, at the end of the one year, you would have $1,050. The fifty dollars would represent interest earned over that period of time.
Now, if you had the same option as above, but opted for a 2-year fixed deposit term, let’s see two ways you can make money.
In the first option, you invest $1,000 at 5% annual interest rate. Therefore, at the end of the first year you make $50 on your investment. Now you re-invest the $1,000 principal and by year-end make another $50.
Therefore, with simple interest, you make a total profit of $100 over two years.
Taking the same example, let’s see how returns are different when you opt for compound interest.
At the end of the first year, you make $50 in interest. But instead of withdrawing this interest, you reinvest it for the second year along with your initial investment of $1000.
So for the second year, you have invested $1,050. Now, at 5% annual interest rate, your investment would be $1102.5. Here $1,000 was your initial investment and your profits are $102.50.
When you compare the simple vs compound interest, you can see that with compounding you made an additional $2.50.
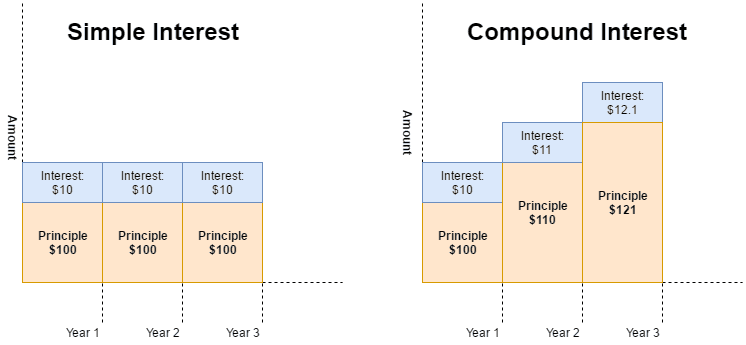
Simple vs Compound Interest
The above picture depicts the difference between simple and compound interest. The example shows that while the interest rate of 10% was applied to both, with simple interest, the $10 interest was paid every year.
By compounding at the same 10% interest, by year 3, the interest earned is $12.10 – 21% more than the fixed 10$ return.
Compounding is simply a process of making more returns on an investment by re-investing the earnings.
Compound interest helps investors or savers to grow their investments exponentially and is particularly advantageous to young investors as time is the greatest variable working in their favor.
The compound interest, which is reported as a percentage refers to the annualized rate of return at which the invested capital has compounded over the period of time.
The formula for annual compound interest is as follows:
Annual compound interest = the future value of the investment including interest
P = Principal amount (initial deposit or initial investment)
r = annual interest rate in decimal (ex: 5% annual interest rate will be expressed as 5/100 or 0.05)
n = the number of times the interest is compounded every year
t = the number of years or duration of the investment
A simpler version of the above formula is also read as:
In this example, the interest is compounded once per period.
For example, if you had an amount of $1,000 in a fixed deposit account that has an annual interest rate of 5% compounded yearly, then the value of the investment after a period of 5 years would be calculated as:
P = $1,000
r = 5% or 5/100 = 0.05
n = 1
t = 5
$1,000 (1 + 0.05/1)^(1 * 5)
$1,000 (1.05)^5
Compounded Interest = $1,000 x 1.276281 = $1,276.28
This value of $1,276.28 can also be reached via the simpler formula where the interest is compounded once per period only.
Compound interest, when expressed in annualized terms is referred as the Compound Annual Growth Rate or CAGR for short.
The CAGR represents the annual growth rate of the investment over a period of time. CAGR is derived by dividing the value of the investment at the end of the period by the value of the investment at the start.
The result is raised to the power of one divided by the period of time and the resulting amount is subtracted by one.
Mathematically, CAGR is calculated as:
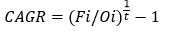
CAGR Formula
Fi = Final value of the investment
Oi = Original value of the investment
t = period of time
If we go back to the example from the previous section, we can calculate the CAGR.
Original value of investment was $1,000; Final value of investment was $1,276.28; period of 5 years
Therefore, CAGR would be [($1,276.28/$1,000)^(1/5)] -1
= [1.27628^0.2] – 1
= 1.05 – 1
= 0.05 or 5%
Therefore, the compounded annual growth rate or CAGR for the investment over the 5 year period is 5%.
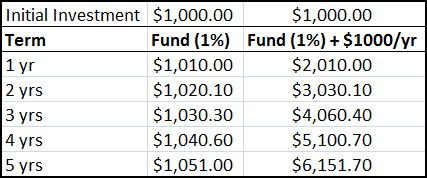
Compound interest examples with two variations
The left side of the table shows an initial investment of $1,000 that gives a 1% annual return. The interest from the first year’s investment is reinvested back into the second year and so on.
The right side of the table depicts the example when an investor adds $1,000 every year.
Two key points from the above table: time and the amount of money invested can greatly increase the returns.
Interest rates play a major role for any type of investing. After all, interest rates set by the central bank become the benchmark for just about anything – from investments to debt.
Compounding can play a big role in certain types of investments where the investor receive regular payouts such as dividends or interest on bonds.
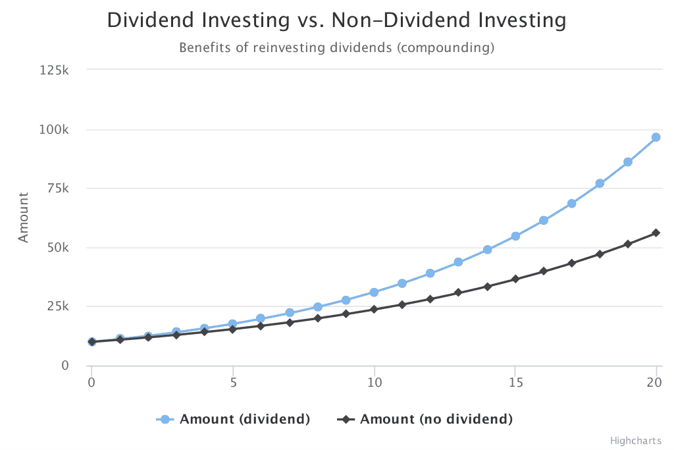
As a rough comparison, if you invested $10,000 in a dividend paying stock with an average annual return of 12% you would have $96,462 at the end of 20 years.
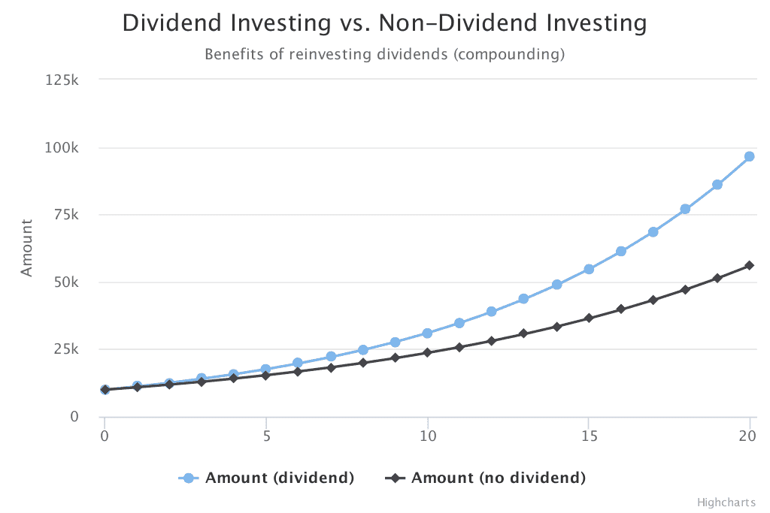
dividend investing vs non-dividend investing
On the same note, if you invested $10,000 in a non-dividend paying stock with the same annual return, it would have given a total return of $56,044, close to half of the amount one would have earned if they had invested in a dividend paying stock.
The above chart compares both the values. As you can see, the power of compounding clearly stands out in certain cases of investments.
Besides dividends, a classic case of compounding the returns is applicable with bank deposits such as savings accounts, fixed-term deposits, and certificates of deposits.
For investors holding bonds, the annual or bi-annual interest payments can be reinvested in purchasing other bonds or other securities. There are also specific bonds such as the zero coupon bonds which automatically include compounded returns.
The tradeoff is you do not get the interest payments but receive the face value of the bond and compounded interest at maturity.
So, we have run through all the numbers, yet this doesn’t feel real for some reason. I mean all of the calculations are real for sure, but how does this really impact our lives?
This is something I want you all to really think about in terms of seeing if you can do this for your family or a worthwhile charitable cause. How do we improve the lives of generations to come long after we are gone?
Simple answer – compounding returns.
Most people go through life working extremely hard to provide for their loved ones but are often unable to make enough to take care of everything and still leave a sizable nest egg.
After you do what’s required to raise your kids, pay for college, pay off your house and save for retirement, there just isn’t much left. If you don’t have kids, don’t worry you still fall in the same boat.
The money you have spent to help aging parents, a health condition, nieces and nephews or a charity close to your heart has also left you strapped.
Regardless of your attachments in life, life has some way of separating you from your money.
This is the first question you need to answer. For me, it’s my great-grandchildren I will likely never meet.
Who do you want to give a headstart to in life? Is it a person or organization doing awesome work to help make the world a better place?
You should definitely give this a lot of thought, but don’t worry – you won’t screw it up.
This is solely up to you again. I apologize as that’s likely not a helpful response. For me, the number is $10,000. However, for you, the number could be much higher or $500 dollars.
The point is that you are helping someone or a cause bigger than yourselves.
Three years gives you enough time to get your act together, but not so much time the goal is not a priority. This timeline breaks down to 36 months.
Now the easy part, let’ s say your goal is $2,500 dollars – this breaks down to 70 bucks per month. Do you see how these large numbers become very manageable once you stretch them out?
If your goal is $500 dollars, then that means you need to set aside about 14 bucks a month.
This is the really easy part. You can invest in the US market. You can do this through a number of means, but for simplification sake, you can buy the SPY ETF which mirrors the price action of the S&P 500.
I’m hoping that you are a fan of movies in order to get this reference. One of my favorite movies as a kid was Back to the Future Part II. In this film, a Western Union man delivers a message to Marty McFly that Western Union had been holding for 70 years. The man said the letter was first delivered to the company in 1855 and was to be delivered to a recipient Marty McFly in 1955.
Still wondering how long you need to keep the money invested? That’s right, you need to keep the money out there for 70 years. Call this an example of life imitating art from the movie.
This means you will likely not be here for the positive response from recipients. You are truly performing this act of giving out of love.
According to this article posted on CNBC, the S&P 500 has returned an average of 9.8% over the last 90 years. So, let’s do some really simple math here.
You can find a number of free investment calculators. I landed on one from investor.gov.
Compound Return Calculator
Let’s say you decide to save that 70 bucks a month for three years and invest the $2,500 dollars. Well flash forward 70 years and the money would have amassed to a whopping 1.7M.
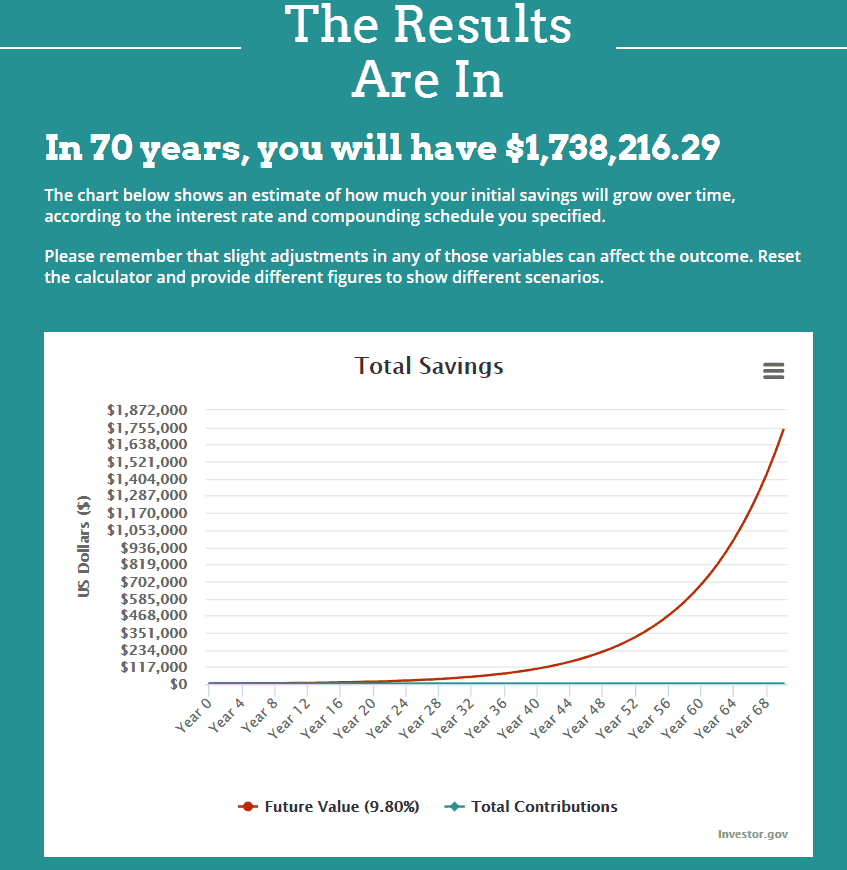
Compound Returns
Now 70 years is pretty far away
Since we are going so far out in the future, a dollar today is not worth a dollar 70 years from now. In actuality, one dollar today will require 5 dollars to buy the same goods and services in 70 years.
So even factoring this rough estimate for adjusting for inflation, you are still leaving behind $350,000 in real dollars. I get that this is an oversimplification of the numbers and I’m doing that intentionally.
The point is you are going to leave someone an unexpected love offering that can help alter the trajectory of their lives.
The $10,000 I am leaving will provide my future generations close to 7M which will be about 1.4 million dollars 70 years from now.
You can always just say “use however you see fit” and that is completely ok. I plan on leaving one stipulation and that is the money should be used towards higher education. Of course, I will need to put in safeguards under a trust to manage all sorts of risks. From market collapse to in-fighting from future heirs.
But I think you get the point.
Provide something to someone out of love that can help them get a jump start on life in order to make this world a better place.
As shown in this article, compound returns are something that investors and consumers need to thoroughly understand.
Building upon this idea, the key aspect of successful compounding investing is time.
Remember life is more than money, but when you don’t have any it can mean the world. Find ways to help your fellow woman and man and a long-term gift is a great way to do it!
Tags:
Day Trader Salary
Trading stocks is a daunting task and turning a profit trading stocks is even more difficult. There are literally thousands of books and articles on the web related to trading and the path to riches....
VIX Futures Overview VIX futures, short for volatility index is one of the most popular derivatives instruments listed on the Chicago Board Options Exchange (CBOE). The VIX futures are also known as...
Investing
“Our favorite holding period is forever.” You can probably guess who said that. Yes, this famous quote is from Warren Buffet, one of the most successful investors of all times. Warren Buffet, Peter...
